paper: 《SmoothQuant: Accurate and Efficient Post-Training Quantization for Large Language Models
》
repo: https://github.com/mit-han-lab/smoothquant

SmoothQuant is a training-free, accuracy-preserving, and general-purpose post-training quantization(PTQ) solution to enable 8-bit weight, 8-bit activation(W8A8) quantization for LLMs.

1 动机

许多实验表明, 对LLM进行量化，激活值会比权重更难量化，因为: LLM会出现系统性的离群点，这些离群点的值通常会比正常值大很多倍, 引入较大的量化误差。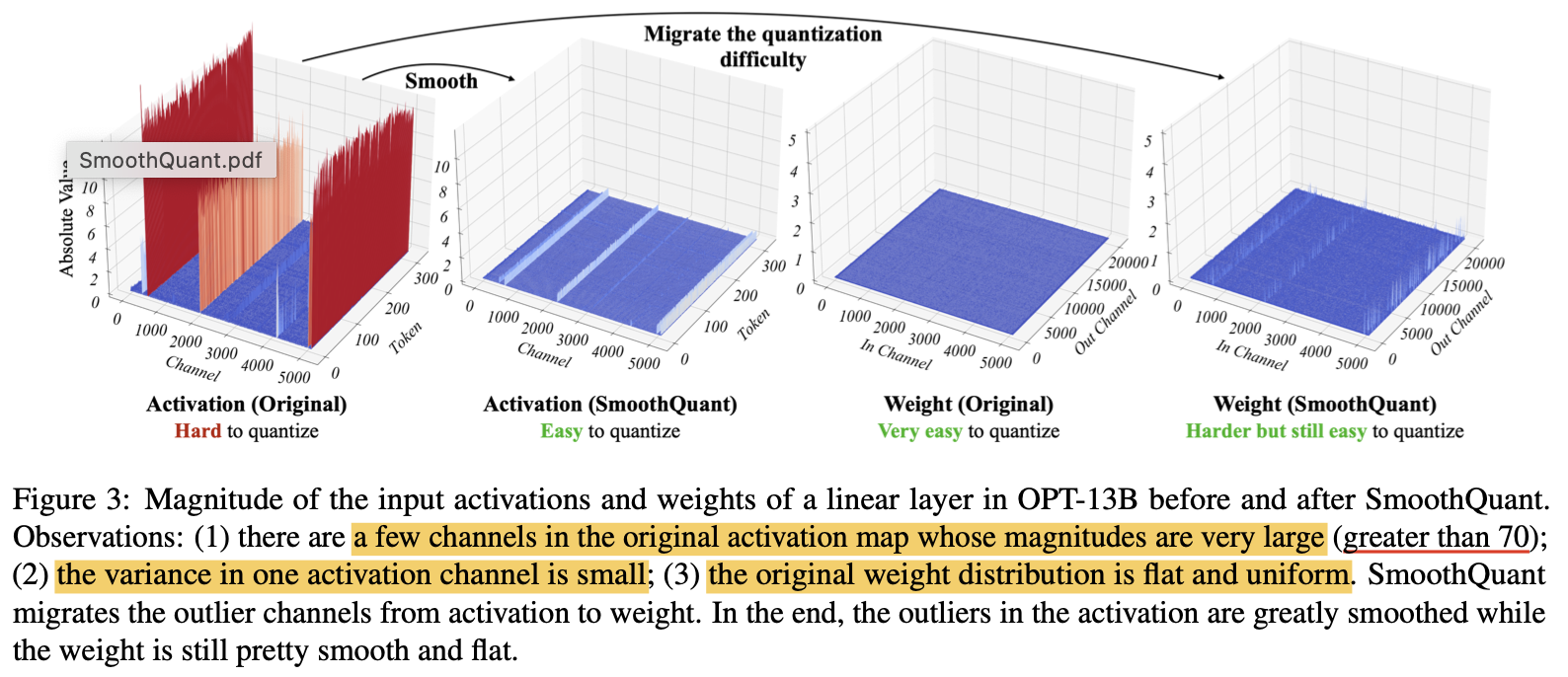

根据论文, LLM激活值和权重的分布具有如下特点：

• 激活值的有些channel会出现系统性离群点, 这些离群点的值通常非常大
• 这些离群点通常出现在某些特定的channel
• 每个channel内的数值方差较小
• 权重的分布相对均匀，即使有离群点, token维度的方差也不大(激活值在token维度的方差较大) [上图标明了token维度和channel维度]

2 方法

2.1 不同粒度的量化

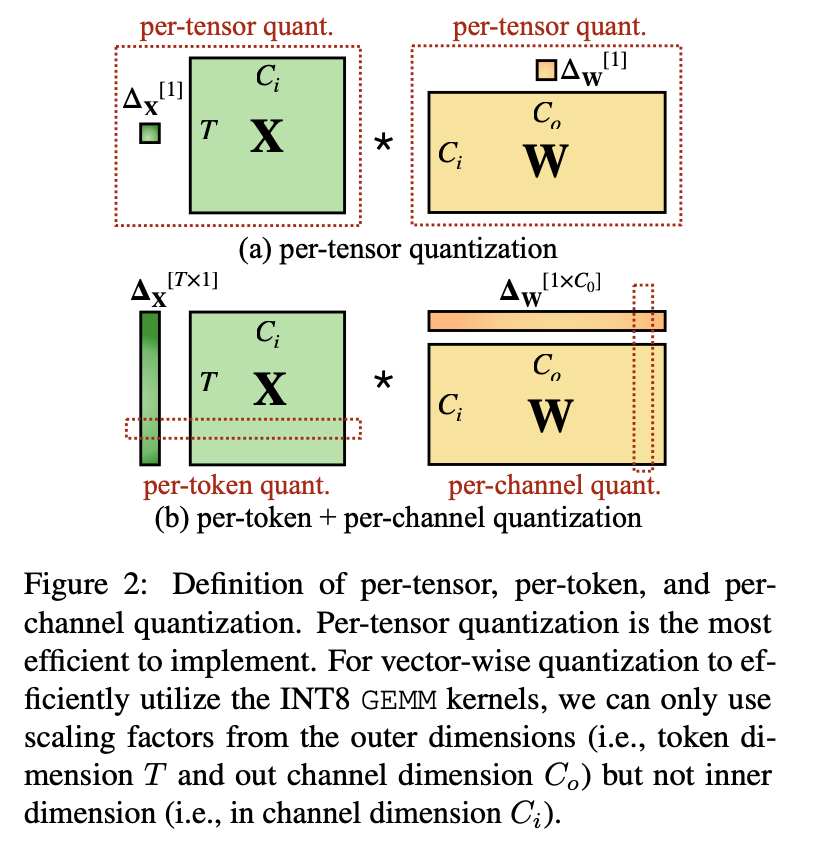
• LLM中大多数激活值的shape可以表示为[B, L, H*D], 所谓per-token对应着L所在的维度，per-channel对应着H*D的维度。
• 上图(b)表示对激活值做per-token量化,对权重做per-channel量化, 它对应的数学表达式可以组织成如下形式
  $$\mathbf{Y}=\operatorname{diag}\left(\boldsymbol{\Delta}{\mathbf{X}}^{\mathrm{FP} 16}\right) \cdot\left(\overline{\mathbf{X}}^{\mathrm{INT} 8} \cdot \overline{\mathbf{W}}^{\mathrm{INT} 8}\right) \cdot \operatorname{diag}\left(\boldsymbol{\Delta}{\mathbf{W}}^{\mathrm{FP} 16}\right)$$
• 对激活值做per-token量化的效果只是略好于per-tensor量化(原因从动机一节也可以理解), 之所以没有直接做per-chnnel量化在于这一操作对硬件并不优化, 论文原文是这样描述的

  However, per-channel activation quantization does not map well to hardware-accelerated GEMM kernels, that rely on a sequence of operations executed at a high throughput (e.g., Tensor Core MMAs) and do not tolerate the insertion of instructions with a lower throughput (e.g., conversions or CUDA Core FMAs) in that sequence.

2.2 SmoothQuant的量化策略

一句话概括SmoothQuant: 通过数学上的等价变换，完成了outlier magnitute migration。这样, 激活和权重的分布都相对flat, 从而可以使用per-tensor量化。

• 首先在Calibration Set上获取激活值的per-cahnnel最大值
• 然后做权重变换
• 最后在变换后的模型上过Calibration Set，确定量化的scale值

2.3 总结

• 如果是原来per-tensor或者per-token的量化, 都是直接对激活值或权重量化
• 在SmoothQuant方案中, 会先对权重进行smooth变换, 然后对变换后的权重进行量化
• migration strength 的选择和具体模型相关, 是一个超参数，若激活值的离群现象严重，应该选取更大的值。
• 对激活值的变换是一个运行时行为, 如果可以的话可以将激活值的变换转移到前一个算子(比如对QVK矩阵计算, 可以将激活值的变换转移到前面的layernomr算子), 对于无法转移的(比如GLU最后一个FC的输入激活值)则需要插入进行激活值变换的算子(一个乘法算子)